Ex1_2

I first started off by running objdump -d to get the assembly code of the binary. From this I found the functions that were most relevant to finding the password for the binary were main and check.

Taking a further look at main :

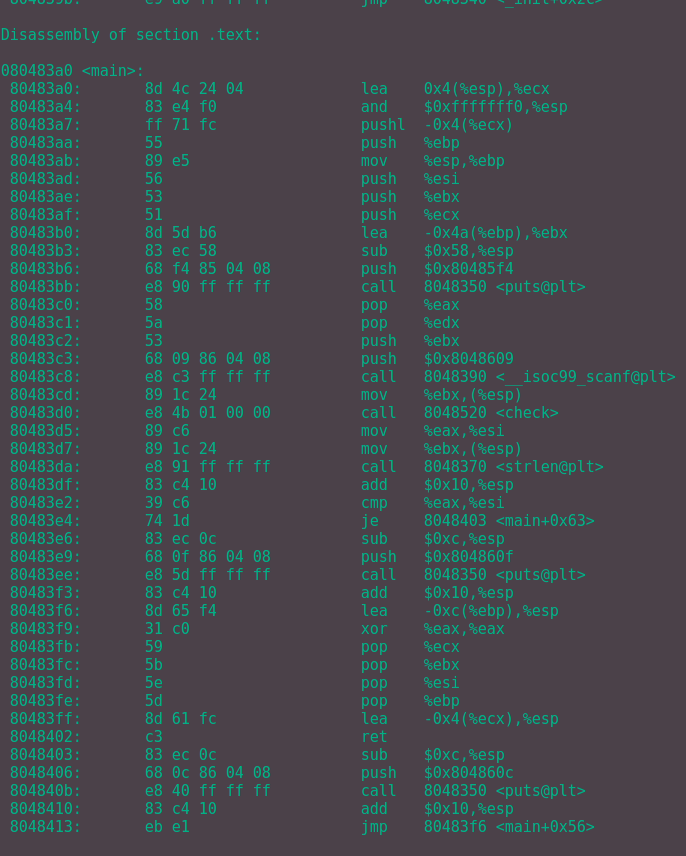Figure 1: Assembly code of main with objdump -d.

After the user has input a string (using the scanf function) of some sort, the check function is called. Then the strlen function is called and a few conditional jumps are performed.

To becodeer understand the control flow of this program, I then used IDA to visualise the program in an easier way.

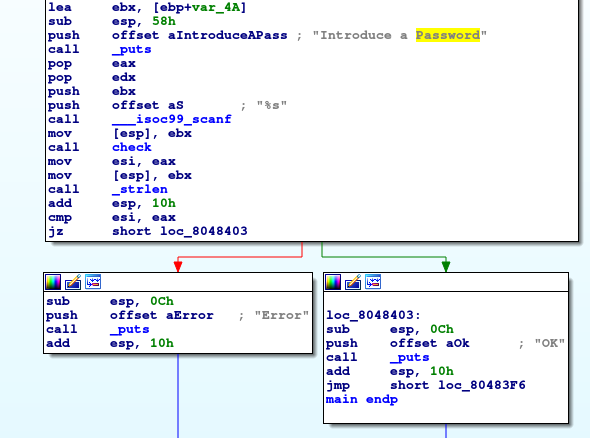Figure 2: Control flow of main in IDA.

From this we can see that before any jumps are made, the value from strlen, which computes the length of the string in ebx(the string the user has entered), is compared with the return value of check. We know this is true because the return value of any function is always stored in eax. Similarly we know that the string the user has entered is stored in ebx since running GDB tells us.

The cmp instruction followed by the jz instruction implies checking the two values are equal. This means in order to enter a correct password for this program, the return value of check must equal the length of the string entered.

Now let us take a deeper look into the check function.

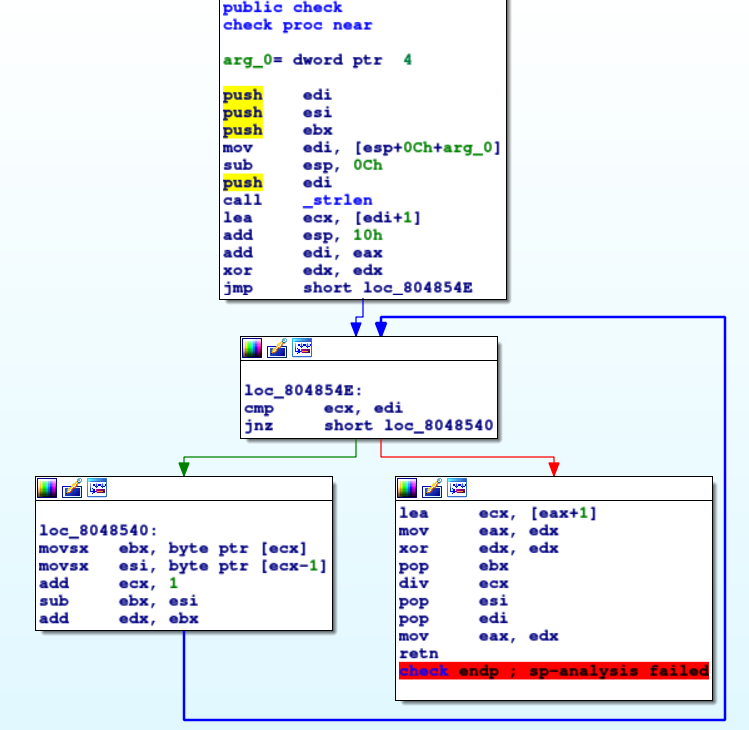Figure 3: Control Flow of check in IDA.

The overall structure of this represents a loop, we know this since we test for a condition, jump, run a block of code and then loop again.

This was where it started to get tricky so in order to understand what was going on I started to use GDB.

I found out that in the loop, the register edi contained the length of the string and ecx was a variable used as a counter variable starting from 0.

In the body of the loop, I found out that the movsx instruction allowed to store 2 adjacent characters of the string entered in registers ebx and esi respectively. In programs, characters are stored as numbers in the ASCII format.

Here is an example of what I mean in GDB:

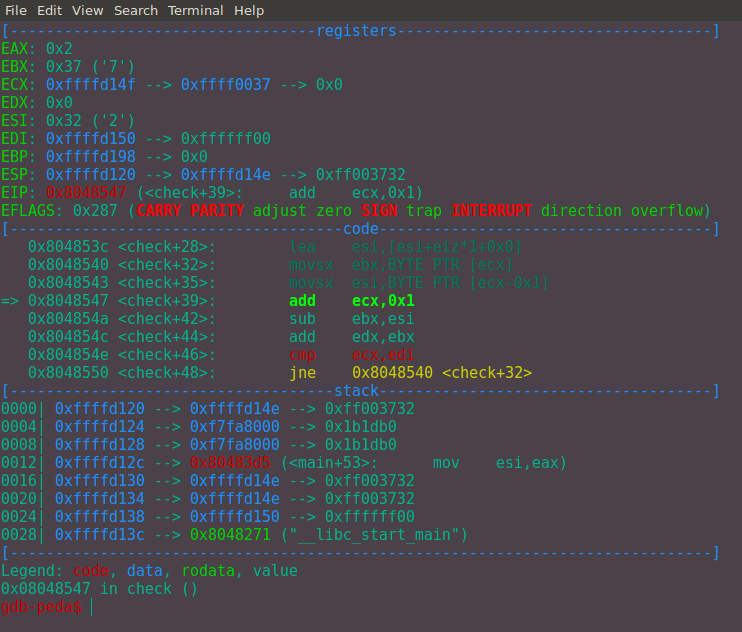Figure 4: Checking values of registers in GDB with input 27.

So in this example ebx would contain 7 and esi would contain 2.

The rest of the assembly in this loop is easy to understand, a running total is kept of the difference between the characters (right character minus left character) and is stored in edx.

In the last block of code, let's work from the end to start to make it easier to explain. In the final mov command we can see that the contents of edx is the what the function returns. So if we can understand what is in edx,we can fully understand the program.

Upon research of the div command, it stores the result of the remainder from the calculation, eax div ecx, in the edx register. Essentially what this means is that edx = eax mod ecx .

We know from earlier that strlen was called on the entered string. This was stored in the register eax. The lea command makes ecx = len(string) + 1 which I double checked with GDB.

One extra thing to note is that the running total from the loop stored in edx is now moved to eax.

So now the puzzle is complete, in summary, this function computes the sum of the differences in adjacent characters \mod len(string) + 1 . This value is then compared to the length of the string in main. If the values are equal, then it is a correct password.

Using mathematics, we can heavily simplify the condition to just:

Any string of length n, c₁ c₂ ... c_n, where:

\[( ASCII(c_n) - ASCII(c_1) ) \mod (n+1) == n\]

Where $ASCII(·)$ gives the ASCII number of a character.

Note that the string can also consist of unprintable characters and still be accepted, for example the string with two hex characters, "\x26\x28", will be accepted by the program.

So overall a final solution could be the number 35. A program to generate a lot of solutions can be given by the following Python code, note that I do not include non printable characters in this.

      import sys
      import string
      from itertools import chain, product

      def bruteforce(charset, maxlength):
          return (''.join(candidate)
                  for candidate in chain.from_iterable(product(charset, repeat=i)
      	            for i in range(1, maxlength + 1)))
      		    LENGTH = 5
      		    string = string.printable
      		    for attempt in bruteforce(string, LENGTH):
      		    	if (ord(attempt[-1]) -ord(attempt[0])) % (len(attempt) + 1)== len(attempt):
      					print(attempt)

My First Crackme (Part 1)

Ex1_2