Solution

This challenge had the fewest solves and the final of the crypto problems I had left. It had around ~280 solves when I solved it. Surprisingly it wasn't that hard to solve, just needed some knowledge of block cipher modes. With that, let's get started.

AES makes use of block ciphers which break the data into blocks and encrypts then with some sort of patterned method. The easiest of the mode of operation, AES-EBC (Electronic Codebook), simply takes each plaintext block and then encrypts them as shown below (and on Wikipedia):

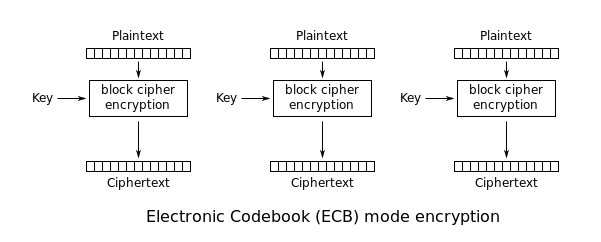
Note that EBC doesn't work well with images in general since a lack of a Initialisation Value (IV), a key and not being to chain cipher blocks together mean that repeated blocks of the same colour will get mapped to the same cipher block. This is bad since the main purpose of cipher texts are about not leaking any useful information. A good example is the Linux mascot, Tux.

In the code given to us:

          
            def aes_abc_encrypt(pt):
                KEY="1234567890123456"

                # ECB occurs here

                cipher = AES.new(KEY, AES.MODE_ECB)
                ct = cipher.encrypt(pad(pt))

                #split cipher into blocks
                blocks = [ct[i * BLOCK_SIZE:(i+1) * BLOCK_SIZE] for i in range(len(ct) / BLOCK_SIZE)]

                #16 random bytes
                iv = os.urandom(16)

                #insert iv into start
                blocks.insert(0, iv)

                # 0-291358 blocks
                for i in range(len(blocks) - 1):
                    #numbers in decimal
                    prev_blk = int(blocks[i].encode('hex'), 16)
                    curr_blk = int(blocks[i+1].encode('hex'), 16)

                    # CBC occurs here
                    n_curr_blk = (prev_blk + curr_blk) % UMAX
                    blocks[i+1] = to_bytes(n_curr_blk)

                #completed cipher text
                ct_abc = "".join(blocks)

                return iv, ct_abc, ct

Keen eyes may be able to spot a combination of EBC and then Cipher Block Cipher (CBC) being used. The CBC mode is used with addition modulo UMAX instead of the regular XOR when chaining the blocks together. Since modulo arithmetic is being used, a reversible operation (we don't care about overflow/losing precision in this problem), we can easily reversed the process to go "back" to ECB. A formula on the Wikipedia page succintly summarises this well: \[P_0 = D_k (C_0) \oplus IV \] \[P_i = D_k(C_i) \oplus C_{i-1} \] Or if you prefer a diagram:

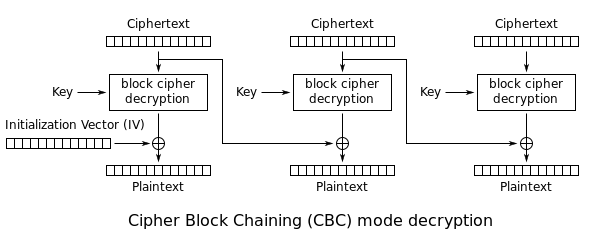
With that, we can start writing some code to reverse the encryption.

        
          def aes_abc_decrypt(ct):
    #split data into blocks
    blocks = [ct[i * BLOCK_SIZE:(i+1) * BLOCK_SIZE] for i in range(len(ct) / BLOCK_SIZE)]

    n = len(blocks) - 2
    for i in range(len(blocks) - 1):
        #calc to perform
        #blocks[n - i] = blocks[n - i] - blocks[n - i - 1]

        prev_blk = int(blocks[n-i-1].encode('hex'), 16)
        curr_blk = int(blocks[n-i].encode('hex'), 16)

        n_curr_blk = (curr_blk - prev_blk) % UMAX

        blocks[n-i] = to_bytes(n_curr_blk)

    ecb = "".join(blocks)
    iv = blocks[0]

    return iv, ecb

And to put it all together, define a function to write the image and call it:

        
          def decrypt():
              with open('body.enc.ppm', 'rb') as f:
                  header, data = parse_header_ppm(f)

              iv, c_img = aes_abc_decrypt(data)

              with open('answer.ppm', 'wb') as fw:
                  fw.write(header)
                  fw.write(c_img)

This results in the following image in ECB mode:

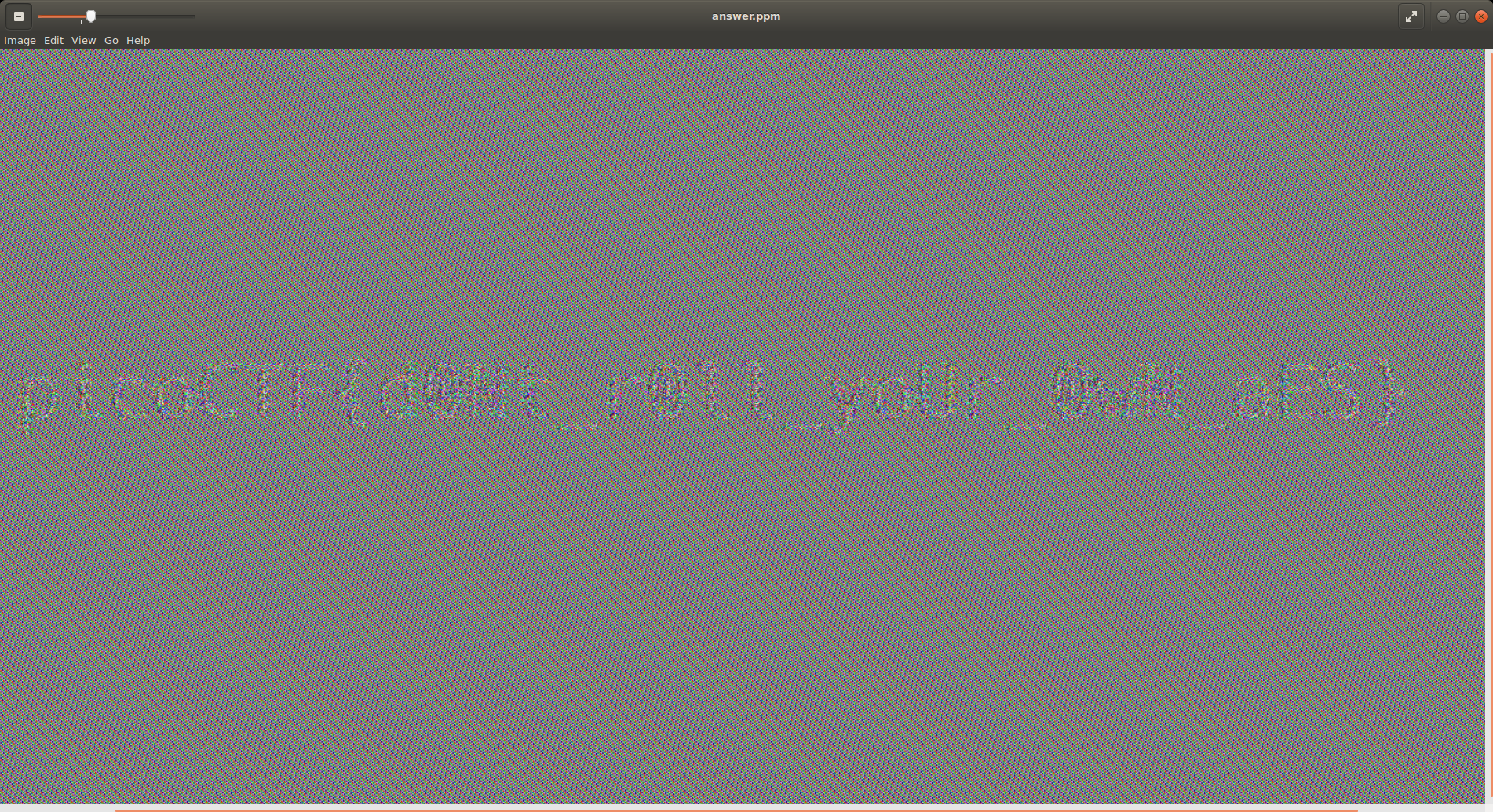
picoCTF{d0Nt_r0ll_yoUr_0wN_aES}

PicoCTF 2019: Crypto - AES-ABC

Problem

Solution